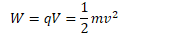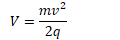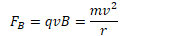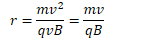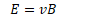Magnetic Fields

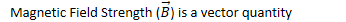
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image342.png

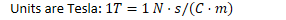
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image343.png

  • 1 Tesla is a very strong magnetic field

  • More common non-SI units is the Gauss

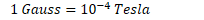
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image344.png

  • Earth's magnetic field strength ≈ 0.5 Gauss

Forces on Moving Charges

  • The magnetic force is always perpendicular to the charged object's velocity, therefore the magnetic force on a moving charge is never applied in the direction of the displacement, therefore a magnetic force can do no work on a moving charge (but it can change its direction)

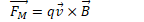
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image345.png

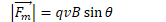
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image346.png

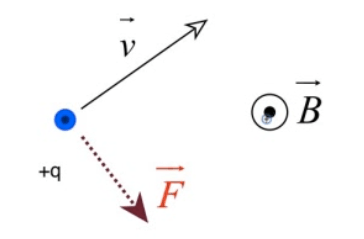
    C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image347.png

Direction of the Magnetic Force

  • Direction of the force given by right-hand rule

    • Point fingers of right hand in direction of positive particles' velocity

    • Curl fingers inward in the direction of the magnetic field

    • Thumb points in the direction of the force on charged particle

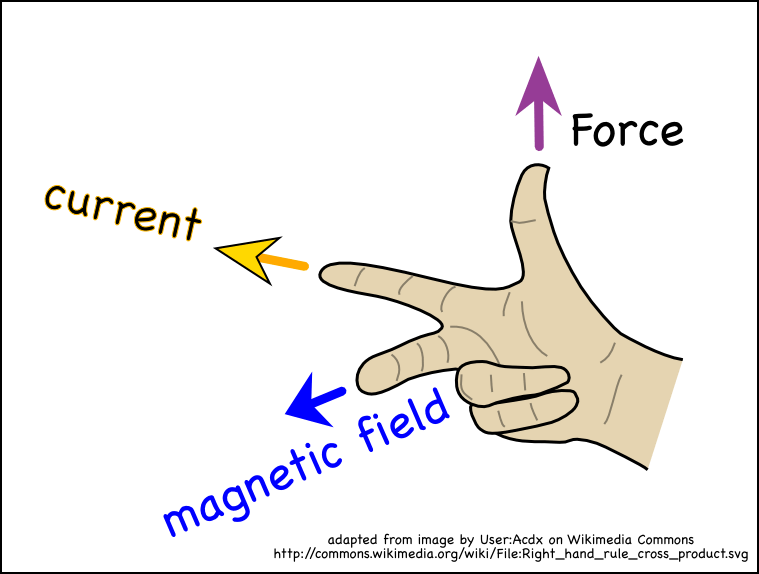
    orc agnetic field

Path of Charged Particles in B Fields

  • Magnetic force cannot perform work on a moving charge

  • Magnetic force can change its direction (moving it in a circle if the magnetic force is constant)

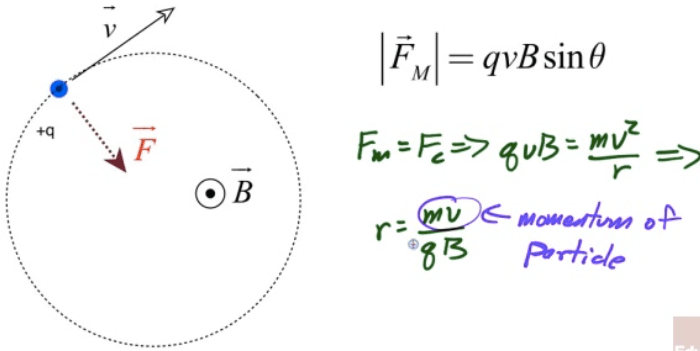
    FM =qvBsin0 و.ع vB$ - عي co; تي بمرا -باايم

Total Force on a Moving Charged Particle

  • E field can do work on a moving charge

  • B filed can never do work on a moving charge

  • Lorentz Force

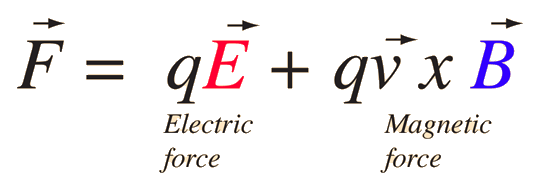
    qE + Electric force Magnetic force

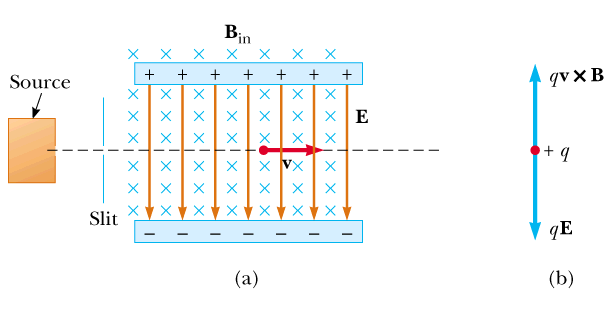
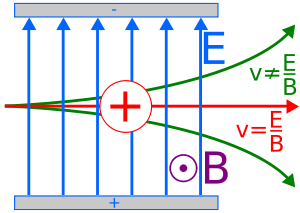
Velocity Selector

  • A charged particle in crossed E and B fields can undergo constant velocity motion is v, B, and E are all selected perpendicular to each other

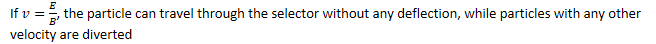
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image351.png

    Source х х х х х х х х х х х х х х х х х х х х х х х х (а) х х х х х х х х х х х х х х х х х х Slit

    ΛλΙΙ

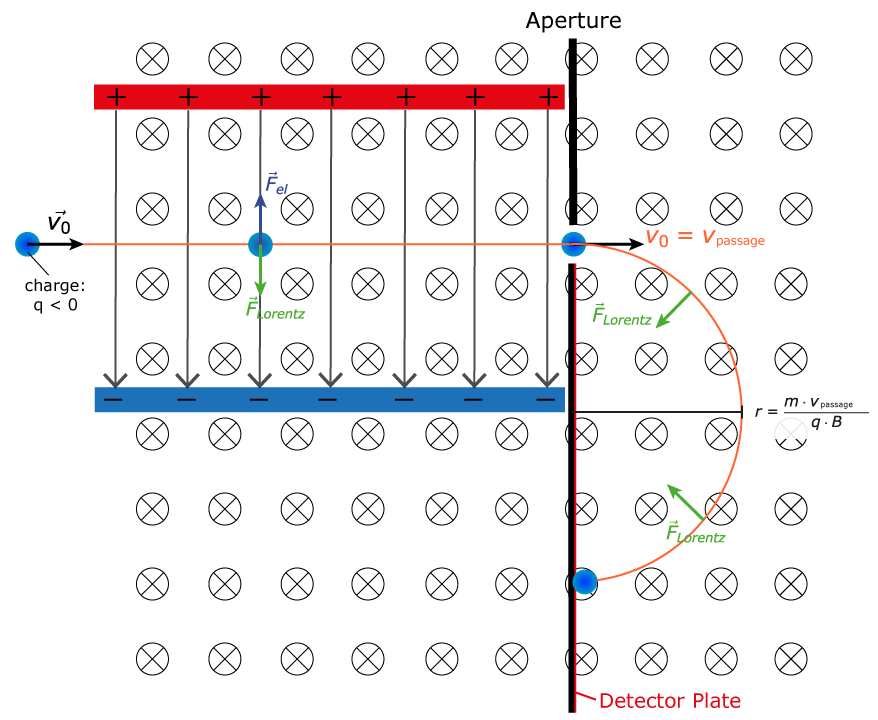
Mass Spectrometer

  • Magnetic fields accelerate moving charges so that they travel in a circle

  • This can be used to determine the mass of an unknown particle!

    0421d 」0400400 ㉨ ㉨ ㉨ A • ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ 각u콤」 ㉨ ㉨ e02552d ㉨ ㉨ ㉨ ㉩ ㉩ ㉨ ㉩ ㉩ 27 uaJ07H 0기 ㉩ ㉩ ㉩ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉩ ㉩ ㉩ ㉩ ㉩ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ ㉨ 각ua〕0 ㉩ ㉨ ㉩ ㉨ ㉩ ㉨ 0 > b :a6」e니0 e」m」adv

Example 1: Velocity Selector

  • Find the speed of a charged particle which passes through a velocity selector with magnetic field strength of 1 Tesla perpendicular to an electric field of 600,000 N/C

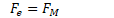
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image355.png

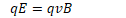
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image356.png

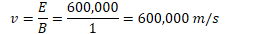
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image357.png

Example 2: Mass Spectrometer

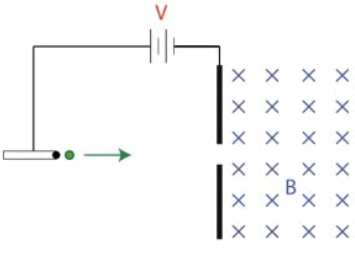
х х х х х х х х х х Х х х х х х х х х х х х х х

  • A proton is accelerated through a potential difference V before passing into a region of uniform magnetic field B as shown

  1. Determine the voltage necessary to give the proton a speed v as it enters the magnetic field region in terms of the proton's mass m, its velocity v, and its charge,

    q.

    • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image359.png

    • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image360.png

  2. Determine an expression for the radius of the proton's motion in the uniform magnetic field

    region

    • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image361.png

    • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image362.png

  1. Sketch the path of the proton in the magnetic field

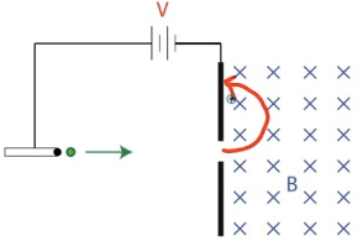
    х х х х х х х х Х х х Х х х х х х Х х х

  2. An electric field is applied in the same region as the uniform magnetic field. Determine the magnitude and direction of electric field required so that the proton passes through the region in a straight line

    • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image355.png

    • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image356.png

    • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image364.png

results matching ""

    No results matching ""